[기초통계] 기술통계 - 확률분포

확률변수의 정의와 역할

사건 (Event)

시행

동일한 상태로 여러 차례 반복할 수 있는 실험이나 관측

사건

시행의 결과로서 나타나는 것으로 한번의 시행에 따른 결과일 수도 있고, 여러번의 시행에 따른 결과일 수도 있다.

 

표본공간 (Sample Space)

통계적 실험에서 모든 발생 가능한 실험결과들의 집합

전사건

표본공간과 동일한 사건

"동전을 두 번 던지는 시행에서 {HH,  HT, TH, TT}"

공사건

아무것도 포함하지 않는 사건

"정육면체 주사위에서 숫자 7이 나올 사건"

근원사건

하나의 결과만 포함

"동전을 두 번 던지는 시행에서 {HH}, {HT}, {TH}, {TT}"

 

확률 변수 (Random Variable)

사건의 시행(동전을 두개 던짐) 결과(HT)를 하나의 수치(1)로 대응(앞면의 개수)시킬 때의 값을 의미한다.
Sample Space 내의 근원사건을 실수값으로 mapping하는 함수의 역할을 하면서도,
확률 분포에 따라 특정한 값이 다시 확률함수의 변수로 활용되는 두 가지 관점이 있다.

 

근원사건을 수치로 Encoding하는 역할을 통해 확률분포에 따라 Encoding된 값이 특정 확률 값으로 mapping될 수 있도록 하는 역할을 한다.

이산확률분포 (Discrete Probability Distribution)

베르누이 분포 (Bernoulli Distribution)

결과가 성공/실패 두 가지로 귀결되는 이산확률분포

 

베르누이 시행 (Bernoulli Trial)

성공/실패와 같이 반드시 시행의 결과가 반드시 두개만 존재하는 랜덤한 실험을 베르누이 시행(Bernoulli trial)이라고 한다.

이항 분포 (Binomial Distribution)

베르누이 시행을 n번 독립적으로 할 때 성공횟수를 확률변수 X로 정의한 이산확률분포

Bernoulli distribution과 Binomial distribution의 관계도

 

다항 분포 (Multinomial Distribution)

여러 개의 값을 가질 수 있는 독립 확률변수들에 대한 확률분포
여러 번의 독립 시행에서 각각의 값이 특정 횟수가 나타날 확률을 정의하는 분포

Multinomial distribution의 probability mass function과 기댓값 & 분산

포아송 분포 (Poisson Distribution)

단위 시간 동안 어떤 사건이 몇 번(x) 발생할 것인지(따라서 rate가 모수)를 표현하는 이산확률분포
단위 시간 외에도 단위 공간이나 단위 면적 등에도 적용할 수 있다.

e.g.) 특정 시간대에 은행창구에 도착하는 고객의 수, 책 한페이지당 오탈자의 수, 하루 동안 사무실에 걸려오는 전화의 수

 

Poisson distribution - rate를 모수로 한다.

이항분포의 포아송분포로의 근사

Binomial distribution을 Poisson distribution으로 근사해 계산할 수 있는 모수 n,p의 조건

이항분포의 두 모수 n과 p에 대해 경험적으로 n이 30 이상이면서 p가 0.05 이하인 경우 이항분포의 계산을 포아송분포로 근사해 계산할 수 있다.

기하 분포 (Geometric Distribution)

기하분포는 "첫 번째 성공" 혹은 "첫 번째 실패" 까지 얼마나 많은 시행(x; not fixed)이 반복되어야 하는가를 묘사하기 위해 사용된다.

 

따라서 가능한 시행의 횟수는 1(처음 바로 성공하는 경우)부터 무한대(계속 실패하는 경우)까지 존재한다.

(e.g.) 동전의 앞면이 처음 등장하려면 동전을 몇 번 던져야 할까?

기댓값 E(X)에 대한 해석은 주사위 눈 1이 나오려면 6번은 던져야한다는 의미이다.

음이항 분포 (Negative Binomial Distribution)

n번째 시행해서 k번째 성공을 관측하는 경우를 묘사한다.

개념적으로는 Geometic Distribution과 유사한 느낌으로 생각해볼 수 있고,

x-1번째 시행까지 k-1번째의 성공을 하고 k번째에 성공을 하는 상황이라고 이해할 수 있다.

x-1번째 시행까지 실패한 횟수는 (x-1) - (k-1) = (x-k) 번 이다.

Geometric Distribution의 Concept + k번째 성공

초기하 분포 (Hypergeometric Distribution)

비복원 추출에서 N개 중 n개를 추출했을 때, 원하는 것 k개가 뽑힐 확률을 나타내는 이산확률분포

 

N : 전체 모집단 개체수, K : 전체 모집단에서 성공의 횟수, n : 전체 시행 횟수, k : 관찰된 성공의 횟수

초기하 분포의 분산은 이항분포의 분산 np(1-p)에 유한모집단 수정계수인 (N-n)/(N-1)을 곱한 값이다.

 

연속 확률 분포 (Continuous Probability Distribution)

연속 균등 분포 (Continuous Uniform Distribution)

두 개의 매개변수 a,b를 받아서 구간 [a,b]범위에서 균등한 확률을 가진다. U(a,b)

Uniform distribution의 p.d.f.와 mean variance

지수 분포 (Exponential Distribution)

Poisson Arrival 사이의 time interval이 Exponential Distribution을 따르게 된다.

사건이 서로 독립적일 때, 일정 시간동안 발생하는 사건의 횟수가 포아송분포를 따르면
다음 사건이 일어날 때 까지의 대기시간(β)에 대한 확률이 따르는 분포이다.

Exponential distribution의 p.d.f.와 mean variance (평균과 표준편차가 같다)

기본적으로 memory-less property로 인해 이전 사건으로 부터 독립적이 되므로 편리한 계산으로 대표적인 예제들에서는 지수분포를 가정하는 경우가 많다.

memory-less property

 

생존분석(Survival Analysis)에서는 Failure의 Poisson arrival을 가정할 때 Time Between Failure가 Exponential distribution을 따르게 되는 예시가 있다.

 

정규분포와 표준정규분포 (Normal Distribution;  Standard Normal Distribution)

표본을 통한 통계적 추정 및 가설검정이론의 핵심이 되는 분포이며, 사회적 자연적 현상에서 접하는 여러 자료들의 분포가 정규분포를 띄는 경우가 많다.

 

표준정규분포는 정규분포를 따르는 확률변수 X를 모평균과 모표준편차를 이용해 정규화한 변환된 확률변수가 따르는 분포이다.

표준정규분포 표를 통해 확률변수의 확률값 계산이 가능하다.(수기 기준)

 

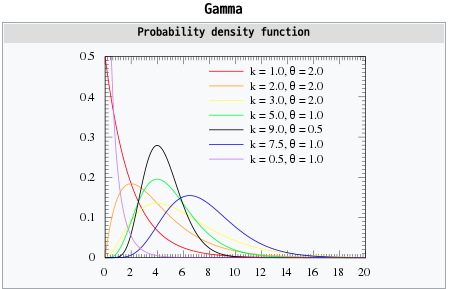
감마분포 (Gamma Distribution)

확률변수 X : 포아송 과정(Poisson Process; θ = 1/λ)에서 k개의 사건이 발생할 때까지의 대기시간
모수(parameter) : k, θ

 

k = 1인 경우 지수분포와 동일한 형태이다. 따라서 감마분포는 지수분포를 한 번의 사건이 아닌 여러 개의 사건으로 확장한 더 큰 개념에서의 분포라고 할 수 있다. 

 

감마분포의 그래프는 rightly-skewed한 형태로 오른쪽으로 긴 꼬리를 가지고 있는 모양이다. (k >= 2 일때)

k가 점점 커질수록 점차 좌우 대칭의 정규분포와 유사한 모양으로 변화한다.

image from wikipedia

α : shape parameter, β : scale parameter

Gamma function은 Factorial 개념을 실수버전으로 확대한 개념이다.

 

카이제곱 분포 (Chi-squared Distribution)

정규분포를 따르는 표본들을 제곱한 다음 합해서 얻어지는 분포

한 집단의 분산을 다루는 분포이다.

가설검정이론의 핵심인 t-분포와 F-분포의 기초가 되는 분포이다.

 

정규분포를 따르는 확률변수 X1, X2, ..., Xk이 서로 독립이라면,

(X1^2 + X2^2 + ... + Xk^2) 은 자유도가 k인 카이제곱 분포를 따른다.

 

카이제곱 분포는 k가 3 이상인 경우부터 봉우리의 모양이 된다. 또한 자유도인 k가 커질수록 대칭 모양의 분포로 접근한다.

 

중심극한정리(CLT)에 따라 iid한 확률변수들의 평균은 대략적으로 정규분포를 따른다.

이에 따라 카이제곱 분포의 표본이 충분히 큰 경우 정규분포로 근사가 가능하다.

 

t 분포 (Student's t-Distribution; X ~ t(n-1))

정규분포의 평균 측정 시에 주로 사용되는 분포이다. 

 

F 분포 (F Distribution; X ~ F(u, v))

카이제곱 분포를 따르는 두 확률변수의 비(검정통계량)는 F 분포를 따른다.

두 집단의 분산을 다루는 분포로 F검정(F-test)이나 분산분석(ANOVA)에서 주로 사용된다.

 

확률 분포의 관계도

아래 사이트를 통해 구체적으로 distribution 사이의 전환 조건들을 상세하게 확인이 가능하다.

 

https://www.math.wm.edu/~leemis/chart/UDR/UDR.html

Univariate Distribution Relationship Chart